Gameplay in Star Versus is rotational in nature. Objects keep track of the direction they’re facing, and move that direction at each step of the engine. This situation requires a bit of trigonometry, most of which can be pre-calculated for efficient runtime performance, though some cannot. In particular, a couple of gameplay elements need to find arctangents, and need to do so quickly.

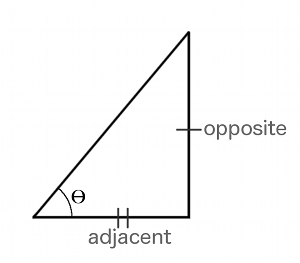
The definition of the arctangent is as follows: given a right triangle, arctan calculates one of the non-right angles using as input the length of the side opposite that angle divided by the length of the adjacent side. In the case of Star Versus, the triangle’s sides are the X/Y distances between two objects, like a projectile and a ship, and the angle is the direction the first needs to travel to reach the second.

Arctan was first needed to figure out when one ship hit another with their sword. Swords don’t have their own collision information, they exist purely as rendering artifacts due to needing animation. Instead, they reuse the code that detects collision between two ships, with a larger hit box to account for the range of the sword. This lets the engine save precious CPU time by calculating the X/Y position deltas only one time. However, it does need to make sure the sword swinger is facing the correct direction, and not attacking away from the target, which is where arctan gets used.

IMPLEMENTATION

An important simplification for Star Versus is that direction is not continuous, but discrete. Objects can only move in 24 possible directions. Moving to the right is 0, up is 6, left is 12, and down is 18. Each single increment of a direction represents an angle of τ / 24 radians. (τ is the fundamental circle constant and equals 6.2831853…)

After the collision detection code runs, we already have the X/Y position deltas for the arctan function. From the signs alone we can tell which of the four quadrants the result is in, so the rest of the code has to find which of the 6 directions within a quadrant is correct, using the absolute values of the deltas.

The 6502 CPU is far too slow to calculate arctan using standard methods, like taylor series, but since the result only needs to be correct to within τ / 24, we can cheat and use an approximation. The overall plan is to first find the radio of X/Y, then imagine a bunch of lines that divide up space to match the possible output directions, next find the slopes of those lines, and compare the ratio to see what direction our angle is closest to.

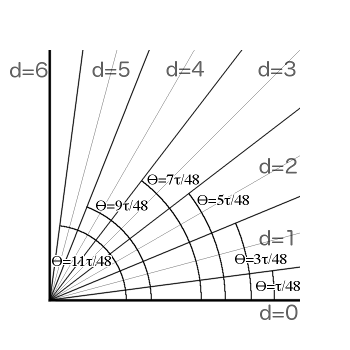
The angles of concern are those that evenly divide the space into regions surrounding the directions the arctan should output. They are τ/48, 3τ/48, 5τ/48, … 11τ/48. Taking the tangent of each of these gives:


tan( 1 * τ / 48) = 0.131652497587
tan( 3 * τ / 48) = 0.414213562373
tan( 5 * τ / 48) = 0.767326987979
tan( 7 * τ / 48) = 1.30322537284
tan( 9 * τ / 48) = 2.41421356237
tan(11 * τ / 48) = 7.59575411273


Because the 6502 does not have multiply or divide instructions, fractional values are not preferable. However, it does have bit shifts that can cheaply divide or multiply by 2. Luckily, the three tangent values above the diagonal are fairly close to 1.25, 2.5, and 7.5, which can be found easily using bit shifts [1]. The other angles below the diagonal are simply reflections, so we can find them by swapping X and Y.

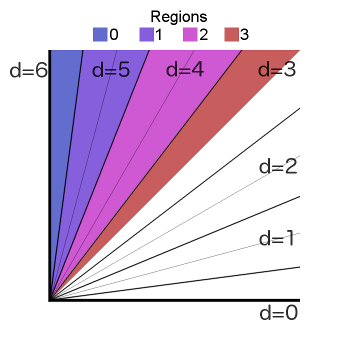
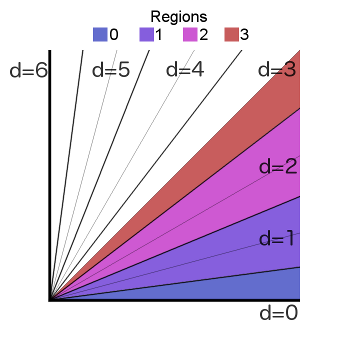
Comparing the X/Y ratio against these target values will produce a region number between 0 and 3. Whether this region is above the diagonal depends on whether X and Y were swapped. Here is some pseudo code for the algorithm:

small, large = x, y
if y < x:
    small, large = y,x
half = small / 2
// compare to 2.5 slope
if small * 2 + half > large:
    // compare to 1.25
    quarter = half / 2
    if small + quarter > large:
        region = 1
    else:
        region = 0
else:
  // compare to 7.5
  if small * 8 - half > large:
    region = 3
  else:
    region = 2
// Use region, whether X/Y were swapped, and quadrant in a lookup table.

The full assembly source is here, with unit tests as well, using nes_unit_testing.

USAGE

After arctan was implemented, it ended up being used all over the place. Aside from sword collisions, bombs also need to home in on their targets. They do this by periodically checking the direction towards the other ship, and adjusting it if they’re slightly off [2]. Circle strafing also uses arctan in much the same way, turning the strafing ship towards the other while moving sideways, creating a circular motion. Although the arctan implementation is imperfect, the error is small enough in practice that bomb homing and circle strafing work well.

During the creation of the single player campaign, the arctan was very helpful for making enemy AI. Basic enemy behavior includes shooting at the player, and the arctan determines how to do this. Different enemies have different bullet patterns, but they’re all based upon the arctan.

As for specific enemies, the Skull travels straight towards the player, using arctan to determine where to go. The Bat prefers to stay at a constant distance from the player, moving in a circle around them, which is accomplished by taking the arctan and then moving a quarter turn away from it. Which direction to quarter turn is randomly determined, and periodically reversed, making a nice flying simulation for the Bat.

The lesson learned is that creating reusable utilities is not only necessary for managing complexity, but can serve as inspiration for future features. Functionality created to solve one single problem can end up influencing a project’s entire direction if it closely matches the given problem domain.

FOOTNOTES

[1] Multiplying the smaller number instead of dividing the larger number has another useful benefit – it helps avoid numerical aliasing, making errors less likely.

[2] Projectiles that home in don’t adjust their direction every single frame, nor do they adjust if they’re too far off target. Doing so would make them far too accurate, negatively affecting game balance.